Conversor de Base Numérica

O que é base numérica?

Base numérica é um conjunto de símbolos que podemos representar um número, ou seja, o principal objetivo de qualquer base numérica é representar os números e por consequência as quantidades.

Cada base numérica tem um propósito especifico, por exemplo a base binária foi criada para o uso de computadores, pois os mesmos só entendem dois estados da informação 0 ou 1. Mais a baixo vamos apresentar as principais bases numéricas.

Imagem com diversos números. — Representação Base Numérica - Fonte: Shuterstock

Quais são as principais bases numéricas?

As principais bases numéricas são o sistema decimal, binário, octal e hexadecimal.

Decimal

O sistema decimal é o mais usado no dia-a-dia , é um sistema de base 10, pois utiliza 10 algarismos para representar a informação, sendo um sistema posicional , no qual a posição do algarismo determina o valor da informação. 0.1,2,3,4,5,6,7,8,9 formam o sistema decimal.

O sistema decimal também é chamado de "sistema de numeração indo-arábico", por ter sido criado pelos hindus e divulgados pelos árabes.

Binário

O sistema binário é composto apenas por 2 dígitos sendo conhecido como um sistema de base 2 . O sistema utiliza o 0 e 1 para formar números, letras, palavras, textos e cálculos. A criação do sistema é atribuída ao matemática alemão Leibniz.

Para converter de Decimal para binário, realiza-se uma série de divisão por 2, utilizando o resto para encontrar os valores em binário.

Exemplo:

Vamos converter o número 14 em decimal para sua representação no sistema binário cujo valor é 1110.

Passo 1: 14 / 2 = 7 resta 0 levamos o 7 para a próxima divisão.

Passo 2: 7 / 2 = 3 resta 1 levamos o 3 para a próxima divisão.

Passo 3: 3 / 2 = 1 resta 1 como já chegamos no 1 de resultado da divisão acabou.

Passo 4: 1 / 2 = 0 resta 1 finalizamos pois o resultado da divisão foi zero.

Passo 5: Enfileirar os restos das divisões na ordem do passo 4 ao 1: 1110₍₂₎

Octal

O sistema octal é composto de oito dígitos para a representação sendo 0,1,2,3,4,5,6,7, sendo conhecido como sistema de base 8.

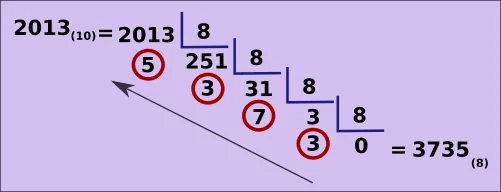
Para converter de decimal para octal basta fazer um divisão por 8 sucessiva até encontrar zero.

Por exemplo vamos converter 2013 em decimal para octal:

Conversão do número 2013 em decimal para octal. — Conversão octal - Fonte: www.google.com

Hexadecimal

O sistema hexadecimal é o sistema de base 16 composto pelos algarismos 0,1,2,3,4,5,6,7,8,9 e as letras A,B,C,D,E,F. O sistema hexadecimal é muito utilizado para representar informações em sistemas computacionais, pois demanda de menos dígitos para representar um mesmo número quando comparado aos sistemas decimal e binário.

Há a possibilidade de se converter um número diretamente de decimal para hexadecimal, mas que envolve um processo mais trabalhoso. Outra forma, é realizar a conversão de decimal para binário e então de binário para hexadecimal. Por exemplo é muito mais simples converter de decimal para binário antes e depois converter para hexadecimal, vamos converter 35 (base 10) em decimal para hexadecimal.

Passo 1: Converter 35 para binário como já mostrado basta dividir sucessivamente por 2, como mostrado anteriormente. O resultado será = 100011 (binário).

Passo 2: Agora vamos dividir esse número em bloco com 4 algarismos do final até o inicio, ou seja teremos 2 blocos o primeiro sendo 0011 e o segundo sendo 10 com dois algarismos. No segundo bloco vamos completar com 0 para também possuir 4 algarismos.

Passo 3: Agora com cada bloco de 4 convertemos para Hexa utilizando a tabela logo abaixo para apoio.

Passo 4: pegando os 2 blocos do fim para o começo temos 0011 que é 3 e 0010 que é 2, ou seja, montando o número é 23 (base16).

Binário	Hexadecimal
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Conversão hexadecimal para binário

Utilize o nosso conversor de Base numérica no início da página para realizar os cálculos de maneira online e grátis!

Conversor de Base numérica

Base numérica